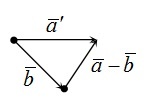Вычитание векторов

Как происходит вычитание векторов

Чтобы вычесть \(\overrightarrow b\) из \(\overrightarrow а\), нужно найти такой \(\overrightarrow с\), сложение которого с вектором \(\overrightarrow b\) составляло бы \(\overrightarrow а\).

Таким образом, формула разности будет выглядеть так:

\(\overrightarrow а-\overrightarrow b=\overrightarrow а+\left(-\overrightarrow b\right)\)

Если задан \(\overrightarrow а\), то можно построить противоположный ему \(-\overrightarrow а\), равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:

\(\overrightarrow а+\left(-\overrightarrow а\right)=0\)

Как производится вычитание векторов по координатам

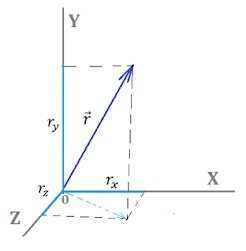
Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из \(\overrightarrow а\) отнимается \(\overrightarrow b\), то из X₁ отнимаем X_2, из Y₁ Y₂ и из Z₁ Z₂.

Проиллюстрируем координатное пространство: 

Основные правила вычисления

Для того, чтобы найти значение разности векторов, можно использовать несколько способов.

Правило треугольника

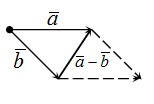
Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор \(\overrightarrow а\), из его начала \(\overrightarrow b\). Тогда вектор, начало которого совпадает с концом \( \overrightarrow b\), а конец — с концом \(\overrightarrow a\), и будет искомым вектором разности \(\overrightarrow a\;-\;\overrightarrow b\). Проиллюстрируем это:

Правило параллелограмма

Если два неколлинеарных, то есть непараллельных вектора \(\overrightarrow а\) и \(\overrightarrow b\) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на \(\overrightarrow а\) и \(\overrightarrow b\), причем начало этой диагонали совпадает с концом \(\overrightarrow b\), а конец — с концом \(\overrightarrow а\). 

Если векторы \(\overrightarrow а\) и \(\overrightarrow b\) заданы в некотором промежутке:

\(\overrightarrow a=\left(а_1;а_2\right),\;\overrightarrow b=\left(b_1;b_2\right)\)

то, чтобы найти координаты их разности \(\overrightarrow a\;-\;\overrightarrow b\), необходимо от точек \(\overrightarrow a\) отнять соответствующие точки \(\overrightarrow b\):

\(\overrightarrow a\;-\;\overrightarrow b=\left(a_1;a_2\right)-\left(b_1;b_2\right)=\left(a_1-b_1;a_2-b_2\right)\)

Проиллюстрируем правило многоугольника:

Примеры задач на понятие разности векторов

Задача 1

Дано

\(\overrightarrow a\;=\left(2;-1\right),\;\overrightarrow b=\left(0;2\right)\)

Найти: \(\overrightarrow с=2\overrightarrow a-3\overrightarrow b\;\)

Решение

Найдем координаты \(2\overrightarrow a\) и \(3\overrightarrow b\). Для этого умножим каждую на два и три: 

\(2\overrightarrow а=2\times\left(2;-1\right)=\left(2\times2;2\times\left(-1\right)\right)=\left(4;-2\right), 3\overrightarrow b=3\times\left(0;2\right)=\left(3\times0;3\times2\right)=\left(0;6\right)\)

Тогда искомый вектор: 

\(\overrightarrow с=2\overrightarrow a-3\overrightarrow b=\left(4;-2\right)-\left(0;6\right)=\left(4-0;\;-2-6\right)=\left(4;-8\right)\)

Ответ: \(\overrightarrow с=\left(4;-8\right).\)

Задача 2

Дано

\(А\left(1;-1;0\right),\;В\left(2;3;-1\right),\;С\left(0;-1;0\right),\;D\left(1;0;2\right)\)

Найти: координаты \(\overrightarrow{AB}-\overrightarrow{CD}.\)

Решение

Для начала найдем проекции \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\).

Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С. 

\(\overrightarrow{AB}=\left(2-1;3-\left(-1\right);-1-0\right)=\left(1;4;-1\right),\;\overrightarrow{CD}=\left(1-0;0-\left(-1\right);2-0\right)=\left(1;1;2\right)\)

Тогда для нахождения координат разности \(\overrightarrow{AB}-\overrightarrow{CD}\), от координат первого вычтем координаты второго:

\(\overrightarrow{AB}-\overrightarrow{CD}=\left(1;4;-1\right)-\left(1;1;2\right)=\left(1-1;4-1;-1-2\right)=\left(0;3;-3\right)\)

Ответ: \(\overrightarrow{AB}-\overrightarrow{CD}=\left(0;3;-3\right)\)