Определение выпуклого четырехугольника

Статья поможет разобраться в свойствах и видах выпуклых четырехугольников. Научит отличать их от невыпуклых фигур. Вы узнаете, как определить, равны фигуры друг другу или нет, найдете ссылки на подробные доказательства всех пунктов равенства.

Что такое выпуклый четырехугольник

Основные свойства

Для начала проверьте наличие четырех вершин, из которых три не лежат на одной прямой. Также должно быть четыре отрезка, которые эти вершины последовательно соединяют. Если все это есть, значит перед нами четырехугольник.

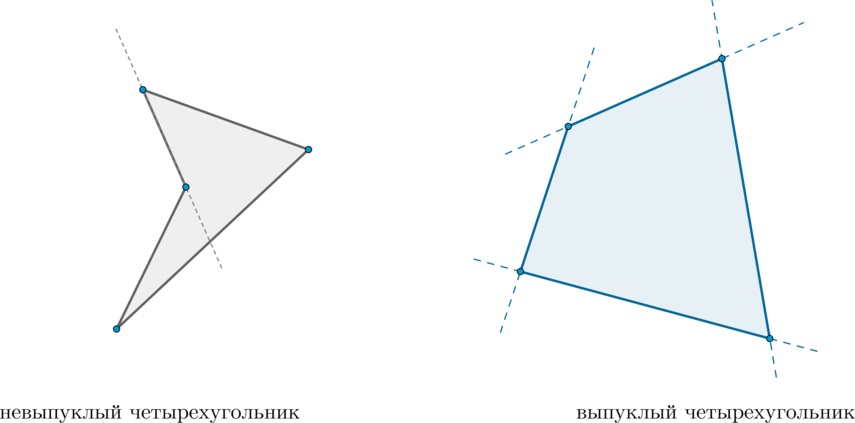
Дальше нужно отличить выпуклый от невыпуклого. Сделать это очень легко - достаточно просто посмотреть на данную вам фигуру: вся она должна быть расположена с одной стороны от любой из своих сторон. На рисунке ниже видно, что для невыпуклой фигуры это условие невыполнимо.

Виды выпуклых прямоугольников

Существуют две большие группы.

1 вид — параллелограммы:

• квадрат,
• прямоугольник,
• ромб,
• параллелограмм.

2 вид — трапеции:

• произвольная,
• прямоугольная,
• равнобедренная. 

 Свойства диагоналей, признаки выпуклости

Можно сказать, что это, за небольшим исключением, одно и то же, поэтому объединим их в один блок.

1 свойство

Пересечение всех диагоналей.

В основе этого свойства лежит соответствующая теорема, но здесь мы ее подробно не рассматриваем.

2 свойство

Любая из диагоналей разделит четырехугольник на 2 треугольника. Можно воспользоваться рисунками, данными в первом блоке статьи, и мысленно провести одну диагональ в каждой из фигур. Результат будет подтверждением написанного в этом пункте.

Еще один признак выпуклости

Если сложить градусные меры всех углов фигуры, получится величина, равная 360º.

Признаки равенства

Выпуклые четырехугольники равны, если у них соответственно равны:

• четыре стороны и один угол;
• три стороны и два угла между ними;
• три стороны и два угла, которые не лежат между этими сторонами;
• три стороны и два противолежащих угла;
• три угла и две стороны между ними;
• три угла и две смежные сороны, которые не лежат между этими углами;
• три угла и две смежные стороны, причем одна из них лежит между этими углами;
• фигуры равны, если площадь одной равна площади другой.

Подробные доказательства по каждому пункту с иллюстрациями можно найти здесь: https://yadi.sk/i/V0X_9c1DY1Wehg 

https://yadi.sk/i/NFnvRwWep3TwKg https://yadi.sk/i/LyoMWkB872mcSQ

Сумма квадратов диагоналей 

Если сумма квадратов диагоналей и сумма квадратов всех сторон фигуры равны, то это параллелограмм. Это свойство относится ко всем видам параллелограмма (ромб, квадрат, прямоугольник, собственно параллелограмм).