Высота трапеции

Что такое трапеция

Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.

Как найти высоту трапеции

Через стороны

Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:

\(h=\sqrt{b^2-(\frac{{(a-d)}^2+d^2+c^2}{2\cdot(a-b)}})^2\)

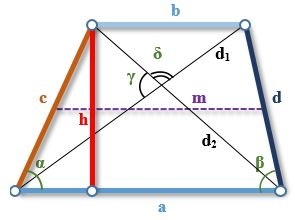
Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.

Через среднюю линию и площадь

Если в условии есть данные о величине средней линии и площади, можем использовать формулу:

\(h=\frac Sm\)

Где m — средняя линия трапеции.

Через боковую сторону и угол

Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:

\(h=c\cdot\sin\left(\alpha\right)\)

Где \alpha — это угол между стороной c и большим основанием a.

Через диагонали, угол между ними и основания

Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:

\(h=\frac{d_1d_2}{a+b}\cdot\sin\left(\gamma\right)\)

Где \(d_1\) и \(d_2\) — диагонали трапеции, а \(\gamma\) — угол между ними.

Через диагонали, угол и среднюю линию

В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:

\(h=\frac{d_1d_2}{2m}\cdot\sin\left(\gamma\right)\)

Через радиус вписанной окружности

Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:

\(h=2r\)

Где r — радиус выписанной окружности.

Примеры вычисления

Задача 1

Дана трапеция, в которой известны основания a и b. Они равны 4,5 см и 2,5 см. Также известны ее боковые стороны d и c, равные 2 см и \(2\sqrt2\) см соответственно. Найти высоту.

Решение

Чтобы решить эту задачу, используем формулу \(h=\sqrt{b^2-(\frac{{(a-d)}^2+d^2+c^2}{2\cdot(a-b)}})^2.\)

Подставляем известные значения:

\(h=\sqrt{2^2-(\frac{{(4,5-2,5)}^2+2^2+{(2\sqrt2)}^2}{2\cdot(4,5-2,5)}}{)^2=}h=\sqrt{4-(\frac{4+4-8}4}{)^2=\sqrt4=2}\) см.

Ответ: h=2 см.

Задача 2

Известно, что основания a и b равнобедренной трапеции равны 3 см и 5 см. Площадь фигуры равна 8 см². Вычислить высоту.

Решение:

Чтобы найти высоту, нужно знать величину средней линии m. Определим ее следующим образом:

\(m=\frac{a+b}2=\frac{3+5}2=4 см.\)

Теперь используем формулу \(h=\frac Sm\) и подставим известные значения:

\(h=\frac84=2\) см.

Ответ: h=2 см.

Задача 3

Мы знаем, что сторона c трапеции равна \(\sqrt2\) см, а угол \(\alpha\) между известной стороной и основанием равен 45 градусов. Найти значение высоты.

Решение:

Используем формулу \(h=c\cdot\sin\left(\alpha\right)\) и подставим значения:

\(h=\sqrt2\cdot\sin\left(45^\circ\right)=\frac{\sqrt2\cdot\sqrt2}2=\frac22=1\) см.

Ответ: h=1 см.

Задача 4

Даны диагонали трапеции \(d_1\) и \(d_2\), равные 2 см и 3 см, а также угол \gamma между ними, который равняется 30 градусов. Основания a и b, длина которых 2 см и 1 см соответственно. Найти h.

Решение:

Для решения задачи использует формулу \(h=\frac{d_1d_2}{a+b}\cdot\sin\left(\gamma\right).\)

Подставим значения:

\(h=\frac{2\cdot3}{2+1}\cdot\sin\left(30^\circ\right)=\frac63\cdot\frac12=1\) см.

Ответ: h=1 см.