Какой многоугольник называется выпуклым
Что такое выпуклый многогольник
Выпуклым называют многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящий через две его соседние вершины.
Или же другой вариант определения:
Выпуклым называют многоугольник, в котором соблюдается следующее условие: если выбрать две произвольных точки, лежащих внутри фигуры, и соединить их отрезком, то все точки этого отрезка так же будут лежать внутри многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примеры
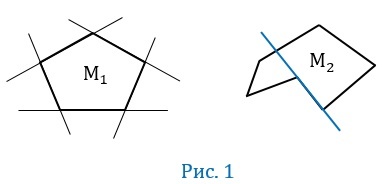
Многоугольник \(М_1\) — выпуклый, а \(М_2\) — не выпуклый.
Сумма углов выпуклого многоугольника
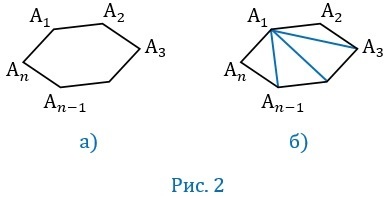
\(A_1A_2A_3...A_n\) — выпуклый многоугольник. Найдем сумму его углов:
\(\angle A_nA_1A_2,\;\angle A_1A_2A_3,\;\angle A_{n-1}A_nA_1,\;...\)
Соединим вершину \(А_1\) с другими. Эти отрезки называются диагоналями. В таком случае образуется n-2 треугольника. Сумма всех их углов будет такой же, как и сумма углов исходного n-угольника. Сумма углов треугольника равна \(180^\circ\), тогда сумма углов многоугольника равна \(180^\circ(n-2)\).
Сумма углов выпуклого n-угольника равна \(180^\circ(n-2)\).
Сумма внешних углов выпуклого многоугольника
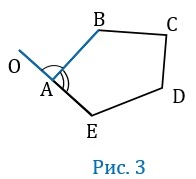
\(\angle OAB\) — внешний угол многоугольника ABCDE при вершине А. (смежный с \(\angle BAE\))
Возьмем по одному внешнему углу при каждой вершине многоугольника \(A_1A_2A_3...A_n\). Тогда их сумма будет равна:
\(180^\circ-A_1+180^\circ-A_2+...+180^\circ-A_n=n\cdot180^\circ-(A_1+A_2+...+A_n)=n\cdot180^\circ-(n-2)\cdot180^\circ=n\cdot180^\circ-n\cdot180^\circ+2\cdot180^\circ=360^\circ\)
Сумма внешних углов выпуклого многоугольника равна \(360^\circ\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так