Как найти высоту треугольника

Что такое высота треугольника

Понятия высоты в треугольнике и прямого угла неразрывно связаны. С помощью применения свойств и формул прямоугольной треугольной геометрической фигуры решают многие задачи в планиметрии. Перед разбором практических примеров следует изучить терминологию. Известно, что треугольником называют форму в геометрии, состоящую из трех отрезков, соединенных тремя точками, которые не принадлежат общей прямой.

Различают несколько видов треугольных объектов, исходя из величин сторон и углов. В зависимости от данного признака в процессе построения высота принимает следующие положения:

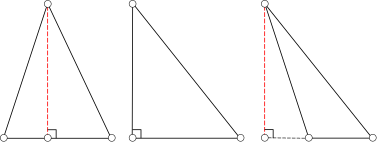
• размещена во внутренней области треугольника, что характерно для остроугольных фигур;
• совпадает с какой-либо стороной, то есть играет роль катета в треугольной форме с прямым углом;
• расположена за пределами геометрической фигуры, если один из ее углов больше 90°.

Ознакомиться с вариантами проведения высоты в геометрической треугольной фигуре можно на рисунке:

Источник: ru.wikipedia.org

С целью обозначения элементов в треугольнике используют буквы латинского алфавита. Рассмотрим пример, когда имеется некий треугольник АВС. При работе со сторонами этого объекта введем следующие уравнения:

a=BC,

b=AC,

c=AB.

В таком случае допустимо сказать, что h_a, h_b, h_c являются высотами, построенными соответственно из вершин А, В, С на стороны, либо линии их продолжающие, с названиями а, b, с.

Как найти: формула

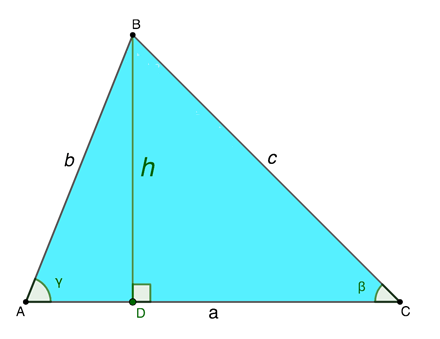
Существует несколько эффективных методов вычисления величины высоты, проведенной в треугольнике того или иного типа. Предусмотрено универсальное математическое выражение для выполнения расчета искомого параметра. В качестве наглядного примера рассмотрим треугольник АВС со сторонами, равными а, b, с соответственно.

 

Источник: microexcel.ru

Если провести в такой геометрической фигуре высоту из вершины В на сторону а, то вычислить ее размер целесообразно таким образом:

• с помощью величины площади S и одной из сторон по формуле: \(h_{a} = \frac{2S}{a}\);
• используя размеры всех составных сторон: \(h_{a} = \frac{2\sqrt{p(p-a)(p-b)(p-c)}}{a}\), где р обозначает полупериметр геометрической фигуры и вычисляется как результат соотношения \(р = \frac{а+b+с}{2}\);
• с применением длины прилегающей стороны и синуса угла: \(h_{a} = b \sin\gamma = c\sin\beta\);
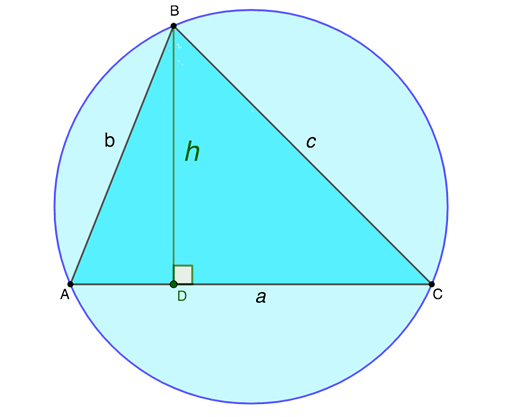
• зная величины сторон и радиус окружности, которая описана вокруг треугольника, по формуле: \(h_{a} = \frac{bc}{2R}\), где R выражает радиус этой окружности.

 

Источник: microexcel.ru

В прямоугольном треугольнике

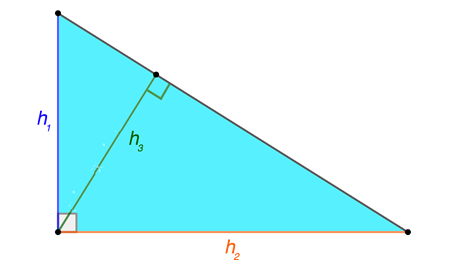
В геометрии к прямоугольным причисляют треугольники, которые обладают одним прямым углом. При этом остальные углы составляют менее 90°, то есть являются острыми. В рассматриваемой фигуре допустимо провести пару высот, совпадающих с катетами. Обозначим такие отрезки за \(h_{1} и h_{2}\).

 

Источник: microexcel.ru

Заметим, что при существующих условиях допустимо построить третью высоту, если вывести отрезок из вершины прямого угла и опустить его на противолежащую сторону. В результате все высоты обладают единой точкой пересечения, называемой ортоцентром. При построении высоты, пересекающей гипотенузу, сформирована пара треугольников, которые являются прямоугольными, подобны между собой и начальной геометрической фигуре. Перечислим несколько формул, актуальных для расчета высоты, построенной к гипотенузе в прямоугольном треугольном объекте:

• \(h = \sqrt{ху}\), где х и у выражают величины отрезков, полученных при делении гипотенузы;
• \(h = \frac{ab}{c}\), если а, b и с равны величинам сторон рассматриваемого треугольника.

В равностороннем треугольнике

Равносторонним называют треугольник, в котором соблюдено равенство всех составляющих сторон. В данной геометрической фигуре высота выполняет сразу несколько функций:

• биссектриса;
• медиана;
• серединный перпендикуляр.

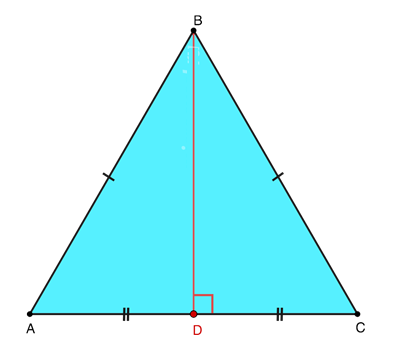
Представим изображение равностороннего треугольника:

 

Источник: microexcel.ru

На рисунке хорошо заметно, что высота BD построена из вершины В и опущена на противолежащую сторону АС. Рассматриваемый отрезок также играет роль медианы, которая высекает из АС два одинаковых элемента AD = DC. Исходя из того, что BD одновременно служит биссектрисой, следует составить равенство образованных углов \(\angle ABD = \angle CBD.\) 

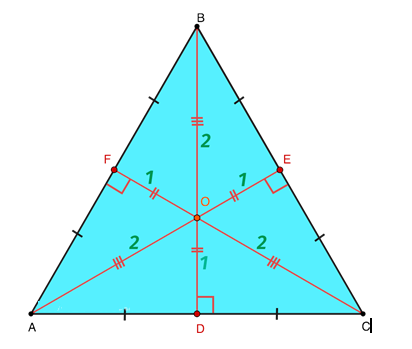
Важное свойство высот в равностороннем треугольнике заключается в соответствии длин. В точке, где рассматриваемые линии пересекаются, их отрезки соотносятся, как 2 к 1, если вести счет от вершины, из которой они выходят. На изображении наглядно представлены следующие математические соотношения:

AO = 2OE

BO = 2OD

CO = 2OF

 

Источник: microexcel.ru

Обозначенный ранее ортоцентр в равносторонней треугольной фигуре служит центральной точкой для окружностей, которые вписаны или описаны около исследуемого треугольника. При этом, сравнивая радиусы таких объектов, целесообразно записать следующее соотношение:

R = 2r

С помощью проведения высоты делят исходный треугольник на пару одинаковых треугольных фигур с точки зрения сравнения полученных площадей. Образованные треугольники имеют по одному прямому углу. В случае построения высот из каждой вершины начального треугольного объекта получим три пары идентичных прямоугольных треугольников.

Представим, что одна из сторон в равностороннем треугольнике составляет а. При таких обстоятельствах определить величину высоты можно с применением следующей формулы:

\(h = \frac{\sqrt{3}a}{2}\)

В равнобедренном треугольнике

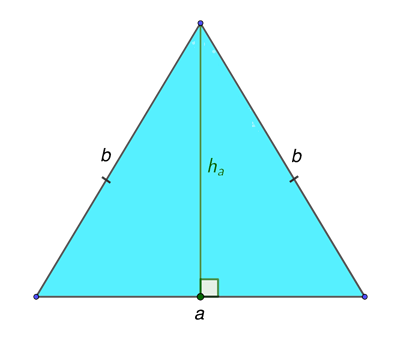
Ключевым отличием равнобедренной треугольной фигуры служит равенство пары сторон. Если построить высоту в таком треугольнике, опирающуюся на основание, то величину отрезка следует вычислять с помощью алгебраического выражения:

\(h_{a}=\sqrt{b^{2}-\frac{a^{2}}{4}}\)

Здесь \(h_{a}\) обозначает высоту треугольника, основание равно а.

 

Источник: microexcel.ru

Свойства высоты

Решение задач на расчет высоты в треугольнике существенно упрощают закономерности, характерные для этого отрезка. В зависимости от вида и особенностей построения выделяют несколько основных свойств. К примеру, в остроугольной треугольной фигуре каждое из оснований высот расположено на сторонах геометрического объекта. В случае с тупоугольным треугольником пара высот находится вне его границ на продолжении сторон.

Источник: egemaximum.ru

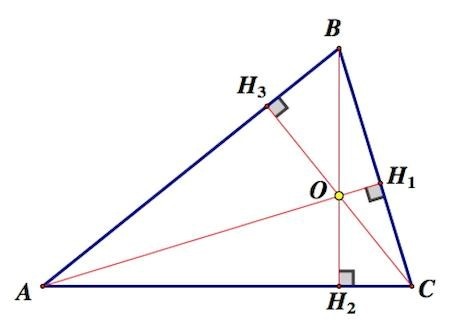
Построенные в треугольном объекте высоты обладают общей точкой пересечения, называемой ортоцентром. Наглядно ознакомиться с данным понятием удобно с помощью следующего изображения, где рассматриваемая точка обозначена за О:

Источник: egemaximum.ru

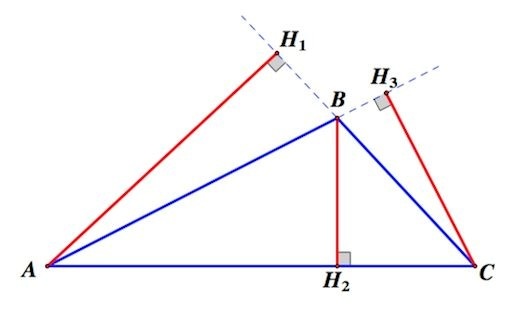
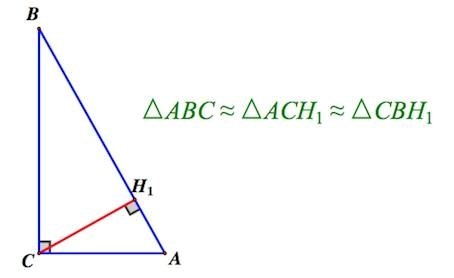
В случае построения высоты в треугольнике с одним прямым углом полученный отрезок делит геометрическую фигуру на пару подобных начальному объекту треугольника. Визуально продемонстрировать озвученное свойство целесообразно графическим способом:

Источник: egemaximum.ru

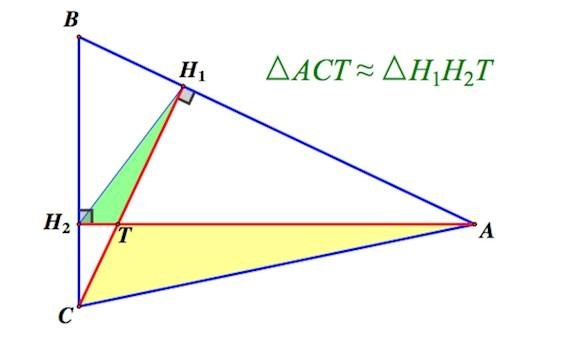
Следующая закономерность посвящена остроугольному треугольнику. В такой геометрической фигуре пара высот образует подобные треугольники.

Источник: egemaximum.ru

Примеры решения задач

Решение

Заметим, что речь в условии задачи идет о прямоугольном треугольнике. Воспользуемся одним из ранее изученных в теоретическом материале свойств, выражающих соотношение между высотой и частями гипотенузы. Запишем справедливую формулу с исходными численными значениями:

\(h = \sqrt{5\cdot 13}\approx 8,06 (см)\)

Ответ: h = 8,06 см.

Решение

Введем обозначения основных элементов фигуры для удобства решения задания. Обозначим катеты за а и b, а гипотенуза пусть соответствует с. Далее обратимся к условию задания и применим теорему Пифагора, что обеспечит быстрый поиск величины гипотенузы через сумму, а именно:

\(с^{2} = а^{2} + b^{2} = 9^{2} + 12^{2} = 225\)

Таким образом, размер отрезка гипотенузы составляет 15 см.

На следующем этапе решения допустимо воспользоваться наиболее подходящим для этого случая свойством высоты треугольника. Составим формулу с подстановкой числовых значений известных величин и рассчитаем искомый ответ:

\(h = \frac{ab}{c} = \frac{9 \cdot 12}{15} = 7,2 (см)\)

Ответ: h = 7,2 см.

Решение

При известных данных целесообразно воспользоваться в процессе решения задания свойством, которое позволяет установить соотношение между высотой, стороной треугольной фигуры и синусом прилежащего угла. Выполним соответствующие вычисления и запишем ответ:

\(h = 7 \cdot \sin 45° \approx 4,95 (см)\)

Ответ: h = 4,95 см.

Решение

В данном случае подходит прием выведения одной формулы из другой. Воспользуемся соотношением для расчета высоты в равнобедренной треугольной фигуре, из которой несложно выразить размер основания. Выполним соответствующие действия с численными значениями величин из условия рассматриваемого примера:

\(а= 2\sqrt{b^{2}-h^{2}} = 2\cdot \sqrt{5^{2}-3^{2}} = 8 (см)\)

Ответ: а = 8 см.

Решение

Из курса теории известно о свойствах высоты в треугольнике с равными величинами сторон, около которого описана окружность. Радиус такой фигуры круглой формы рассчитывают, как \(\frac{2}{3}\) части высоты h. В результате получим следующее справедливое равенство:

\(h = \frac{7}{2} \cdot 3 = 10,5 (см)\)

Зная высоту в равностороннем треугольнике, несложно определить значение его стороны. Составим соответствующую формулу с подстановкой численных значений из условия и запишем искомую величину в ответ:

\(а = \frac{2h}{\sqrt{3}} = \frac{2\cdot 10,5}{\sqrt{3}}\approx 12,12 (см)\)

Ответ: а = 12,12 см.