Теорема взаимного расположения прямой и окружности
Три случая расположения прямой и окружности
Окружность — геометрическая фигура, состоящая из множества точек плоскости, удаленных от заданной точки (центра окружности) на одинаковое расстояние.
Взаимное расположение прямой и окружности зависит от расстояния между центром окружности и данной прямой.
Прямая касается окружности
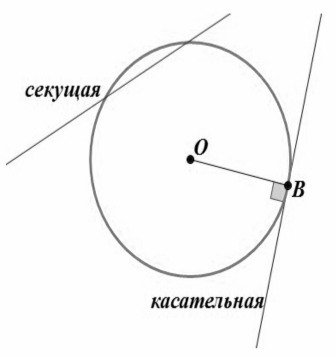
Если прямая и окружность имеют одну общую точку (точку касания), то говорят, что прямая касается окружности и называется касательной.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
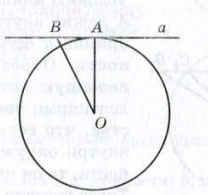
Теорема: если расстояние от центра окружности до прямой равно радиусу окружности, то эта прямая называется касательной к окружности.
Доказательство: пусть расстояние от центра Ο окружности до прямой α равно радиусу R окружности (см. рисунок 1). Проведем из центра Ο перпендикуляр ΟA на эту прямую. Тогда ΟA = R. Для любой другой точки B на прямой α наклонная ΟB будет больше перпендикуляра ΟA, значит, больше R. Из этого следует: расстояние от любой точки прямой α, отличной от A, до центра Ο больше R. Это значит, что прямая α и окружность имеют одну общую точку A, т.е. прямая касается окружности.
Следствие: касательной к окружности называется прямая, проходящая через одну из ее точек и перпендикулярная радиусу, проведенному в эту точку.
Прямая не касается окружности
Прямая и окружность могут не иметь общих точек.
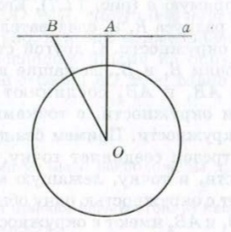
Теорема: если расстояние от центра окружности до прямой больше радиуса окружности, то у таких прямой и окружности нет общих точек.
Доказательство: пусть расстояние от центра Ο окружности до прямой α больше радиуса R (см.рисунок 2). Проведем из центра Ο перпендикуляр ΟA на эту прямую. Получим ΟA > R. Для любой другой точки B на прямой α наклонная ΟB будет больше перпендикуляра ΟA, и следовательно, больше R. Таким образом, расстояние от любой точки прямой α до центра Ο больше R. Значит, прямая α и окружность не имеют общих точек.
Прямая и окружность пересекаются
Осталось рассмотреть случай, когда окружность и прямая имеют две общие точки. В этом случае прямая называется секущей.
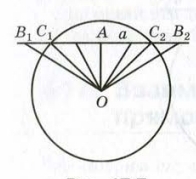
Теорема: если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются.
Доказательство: пусть прямая α не проходит через центр окружности. Опустим из центра окружности Ο перпендикуляр ΟA на прямую α (см. рисунок 3). Его длина по условию меньше радиуса R, следовательно, точка A лежит внутри окружности. С другой стороны на прямой есть точки B1 и B2 , лежащие вне окружности. Отрезки AB1 и AB2 соединяют точку A, лежащую внутри окружности, с точками B1 и B2 , лежащими вне окружности.
Примем без доказательства: если отрезок соединяет точку, лежащую внутри окружности, и точку, лежащую вне окружности, то он имеет с окружностью одну общую точку. Тогда отрезки AB1 и AB2 имеют с окружностью общие точки C1 и C2 , которые являются искомыми точками пересечения прямой α и окружности.
Теоремы взаимного расположения прямой и окружности
1. Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.
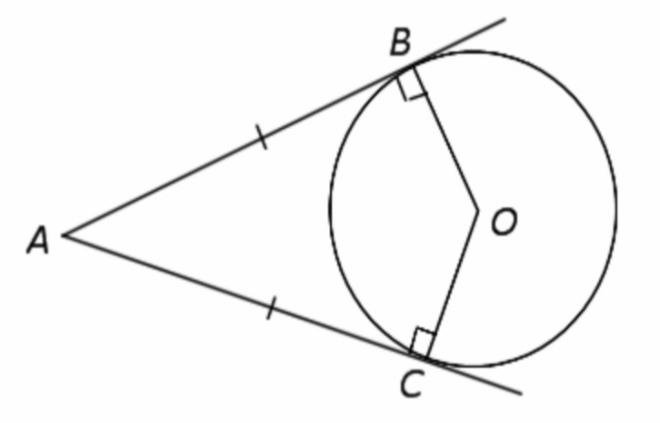
2. Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке: AB = AC.
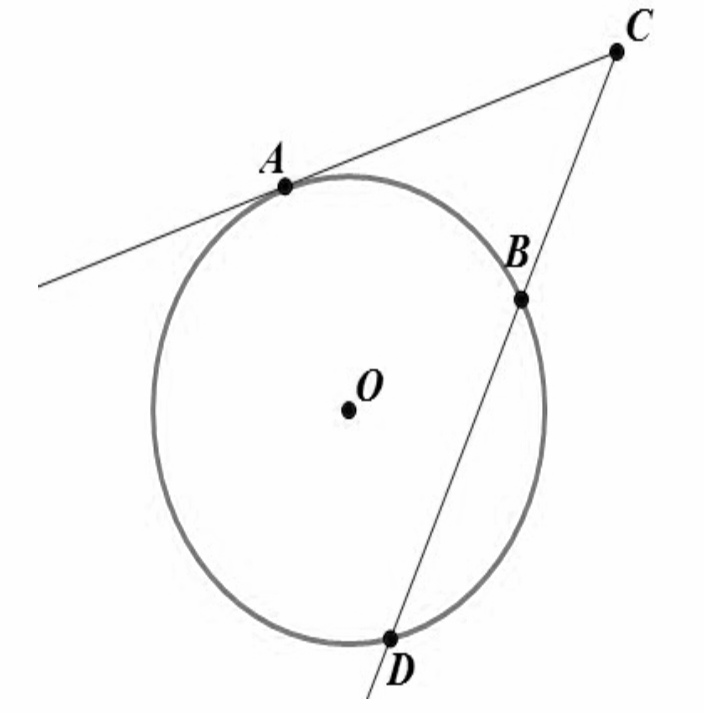
3. Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть: AC2 = CD×BC.
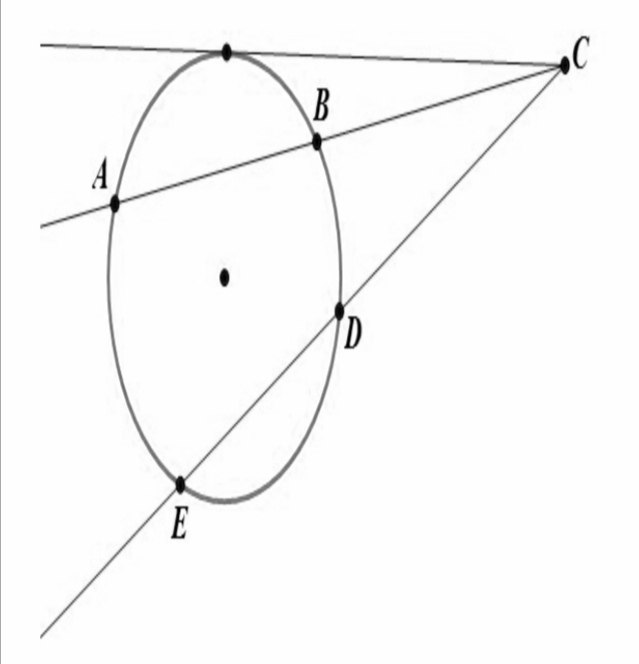
4. Произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть: AC×BC = EC×DC.
Пояснение на примерах
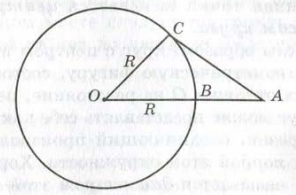
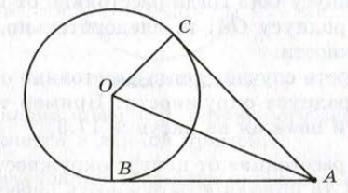
Точка А расположена вне окружности радиуса R и удалена от центра О этой окружности на расстояние d. Чему равно наименьшее расстояние от точки А до точек данной окружности?
Пусть В — точка пересечения окружности с от резком ОА. Покажем, что расстояние АВ является наименьшим из возможных от точки А до точек окружности. Действительно, для любой другой точки С окружности выполняется неравенство : АВ + ВO < АС + СO. Так как ВО = СО = R, получим АВ < АС. Учитывая, что АО = d, ВO = R, получаем, что искомое наименьшее расстояние равно длине отрезка АВ = d − R.
Из одной точки проведены две касательные к окружности. Докажите, что отрезки касательных, заключенные между этой точкой и точками касания, равны.
Рассмотрим две касательные к окружности с центром в точке О, проведенные из точки А, и касающиеся окружности в точках В и С. Треугольники АОВ и АОС — прямоугольные, ОВ = ОС, сторона АО — общая. По признаку равенства прямоугольных треугольников они равны. Следовательно, АВ = АС.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так