Взаимное расположение прямой и плоскости в пространстве

Понятие плоскости и ее обозначения

Понятие плоскости

Плоскости окружают нас со всех сторон. Примеры плоских поверхностей: стол, стены, пол и потолок, школьная доска, скамейка, экран, грани карандаша. Плоскость — одно из важнейших понятий геометрии и стереометрии, математики давно пытаются дать ее точное определение.

Евклид (III век до н. э.): «Поверхность есть то, что имеет только длину и ширину», «плоская поверхность есть та, которая одинаково расположена относительно прямых линий, на ней лежащих».

Фурье (1768-1830): «Плоскость есть геометрическое место всех прямых, перпендикулярных к данной прямой в данной на ней точке».

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Лежандр (1752-1833): «Плоскость — это поверхность, с которой прямая, имея с ней две общие точки, совмещается всеми своими точками, где бы на плоскости ни были взяты эти точки».

Обозначение плоскости

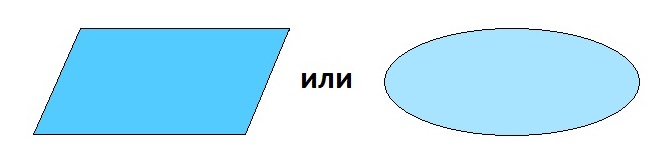
Невозможно изобразить объект, бесконечно простирающийся в длину и ширину. Поэтому для плоскости приняты условные обозначения. На рисунке вместо плоскости изображают ее часть: параллелограмм или «облако» — овал, область с неровными краями.

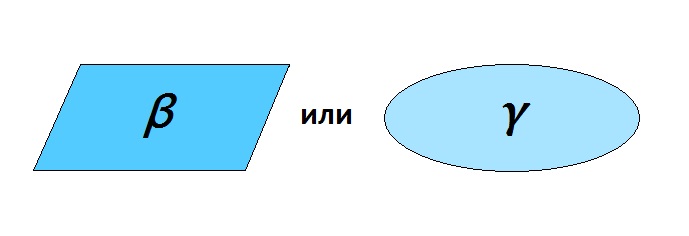
Плоскость обозначают строчными буквами греческого алфавита: α (альфа), β (бета), γ (гамма) и т.д.

Как выяснить взаимное расположение прямой и плоскости

 Есть три варианта взаимного расположения прямой и плоскости в пространстве:

1. Прямая и плоскость пересекаются. 
2. Прямая принадлежит плоскости (лежит в ней).
3. Прямая и плоскость параллельны. 

 Рассмотрим каждый вариант подробней.

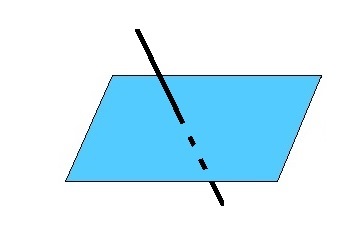
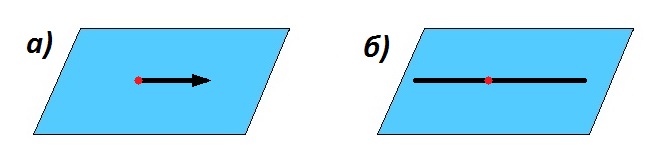
Прямая пересекает плоскость

Прямая и плоскость пересекаются, если они имеют только одну общую точку.

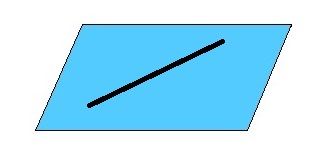
Прямая принадлежит плоскости

Прямая принадлежит плоскости (лежит в плоскости), если все точки прямой лежат в плоскости. При этом достаточно, чтобы две любые точки данной прямой лежали в данной плоскости. 

Аксиома 1

Все точки прямой лежат в плоскости, если хотя бы две точки данной прямой лежат в данной плоскости.

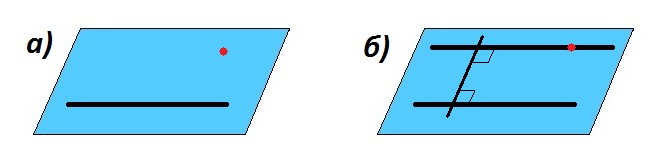
Прямая параллельна плоскости

Прямая, не лежащая в плоскости, пересекается с плоскостью или параллельна ей. Прямая и плоскость параллельны, если они не имеют общих точек. Отсутствие общих точек — признак параллельности прямой и плоскости.

Различные способы задания прямой на плоскости

Положение прямой определяют:

1. Две заданные точки. Через две точки можно провести только одну прямую. Поэтому координаты точек в прямоугольной системе координат задают отрезок или прямую.

2. Точка, через которую она проходит, и параллельная прямая.
3. Точка и направляющий вектор.

4. Точка и перпендикулярная прямая.

Как найти угол между прямой и плоскостью

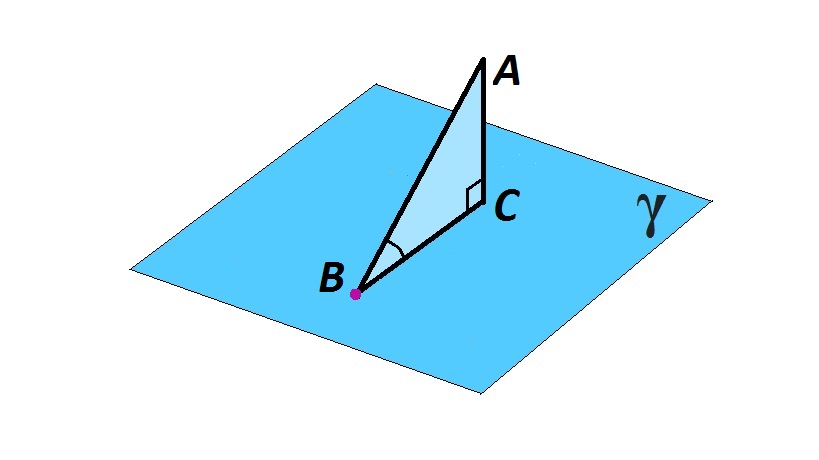
Чтобы найти угол между прямой и плоскостью, нужно знать, каков угол между прямой и ее проекцией на эту плоскость.

На изображении прямая АВ пересекает плоскость γ, и является наклонной к этой плоскости. Проведем перпендикуляр АС. ВС — проекция наклонной АВ. Угол между АВ и γ будет равен ∠АВС прямоугольного ΔАСВ.