Каким может быть взаимное расположение двух прямых на плоскости
Существует три варианта взаимного расположения двух прямых в пространстве: прямые могут
быть пересекающимися, параллельными и скрещивающимися. Изучение этих положений необходимо в начертательной геометрии.
Пересекающиеся прямые
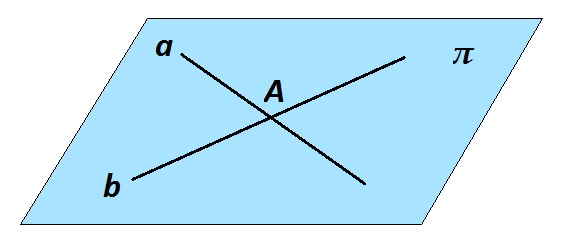
Две различные (то есть не совпадающие) прямые, имеющие единственную общую точку, называются пересекающимися.
Если две прямые имеют две общие точки, то они совпадают.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На рисунке изображены прямые a и b, которые пересекаются в точке А. Через две пересекающиеся прямые проходит плоскость, причем только одна.
Параллельные прямые
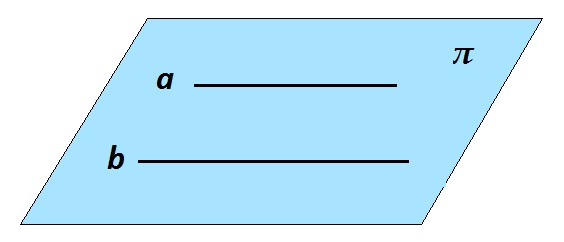
На плоскости прямые параллельны, если они не пересекаются. То есть главный признак — это отсутствие общих точек. Однако для параллельности в пространстве этого условия недостаточно.
Две прямые в пространстве параллельны, если они обе лежат в одной плоскости и не пересекаются. Два отрезка, лежащие на параллельных прямых, также параллельны.
На рисунке a || b, через них проходит единственная плоскость.
Две различные прямые, параллельные третьей прямой, параллельны между собой.
В виде формулы это выглядит так: a||b, b||c ⇒ a||c.
Скрещивающиеся прямые
Через две пересекающиеся или параллельные прямые можно провести плоскость, и притом единственную. Возможна также ситуация, когда через две прямые плоскость провести нельзя.
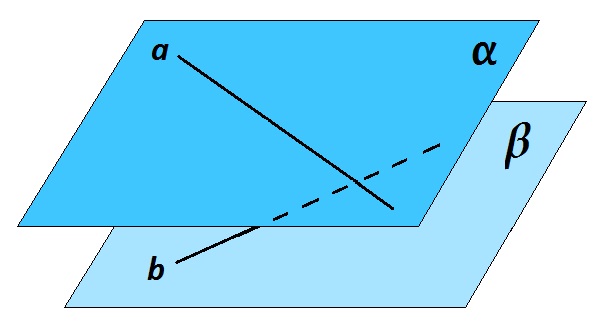
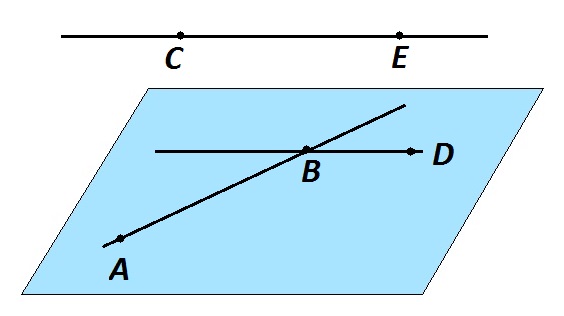
Две прямые называются скрещивающимися, если они не параллельны и не пересекаются.
Другими словами, две прямые скрещиваются, если они не лежат в одной плоскости, так как прямые, лежащие в одной плоскости, обязательно будут либо пересекаться, либо параллельны.
Прямые a и b на рисунке скрещиваются. Важно, что через две скрещивающиеся прямые можно провести две параллельные плоскости. Причем это единственная пара плоскостей.
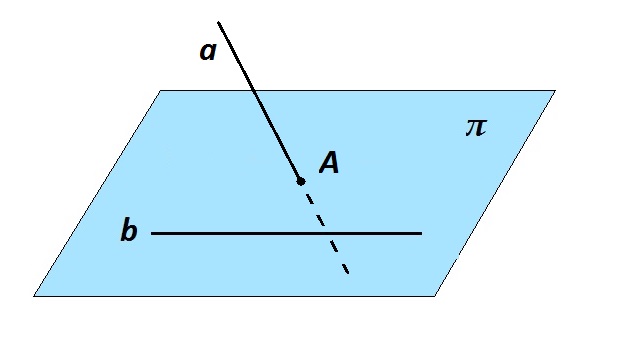
Если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые — скрещивающиеся.
Доказательство:
Пусть a и b — прямые, b лежит в плоскости π, a пересекает плоскость π в точке A. А не принадлежит прямой b. Используем метод доказательства от противного. Предположим, что прямые a и b лежат в одной плоскости. В этом случае данная плоскость проходит через прямую b и точку А, то есть она совпадает с плоскостью π.
Прямая a не может одновременно находиться в плоскости π и пересекать ее в одной точке, как дано по условию. Теорема доказана.
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство:
Рассмотрим скрещивающиеся прямые AB и CЕ.
- Через точку D можно провести прямую ВD параллельную СЕ.
- Через пересекающиеся прямые BD и AB можно провести плоскость.
- Так как прямая CE не лежит в этой плоскости и параллельна прямой BD, то она параллельна и данной плоскости. Эта плоскость единственная.
Теорема доказана.
Полуплоскости. Сонаправленные лучи
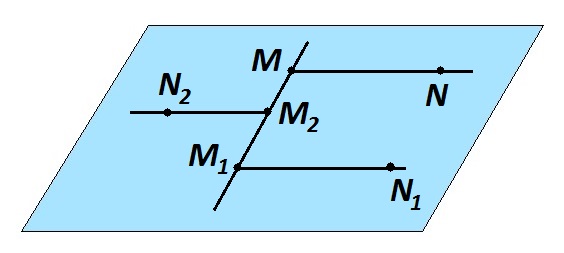
Любая прямая делит плоскость на две полуплоскости.
Лучи называют сонаправленными, если они лежат в одной полуплоскости и параллельны.
Параллельные и лежащие в разных полуплоскостях лучи не являются сонаправленными. На рисунке лучи MN и \(M_1N_1 \)— сонаправленные, а MN и \(M_2N_2, M_1N_1\) и \(M_2N_2\) — параллельны, но не сонаправлены.
Два угла равны, если две их стороны соответственно сонаправлены.
Доказательство:
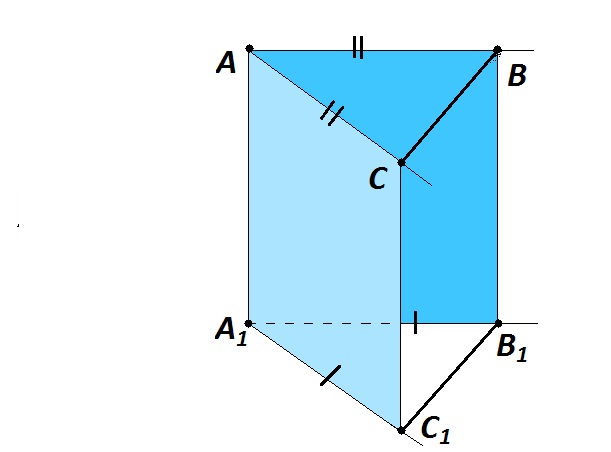
Приведем доказательство для углов, лежащих в разных плоскостях. Изобразим ∠А и \(∠А_1 \)на чертеже.
- Сонаправленные лучи параллельны ⇒ соответственно параллельны стороны углов. Так как через параллельные прямые можно провести единственную плоскость, проведем через них две плоскости. На сторонах угла А и угла А1 отметим точки С, В и С1, В1 соответственно — так, чтобы \(АС=А_1С_1\) и \(АВ=А_1В_1\). Получившаяся объемная фигура имеет вид треугольной призмы.
- У полученного четырехугольника \(AВВ_1A_1\) противолежащие стороны AВ и \(A_1В_1\) равны и параллельны по условию. Это значит, что \(AВВ_1A_1\) — параллелограмм. \(AA_1 =ВВ_1, AA_1||ВВ_1\).
- Аналогично выясним, что \(AСС_1A_1\) — параллелограмм, и \(СС_1=АА_1, СС_1||АА_1\).
- \(СС_1\) и \(BB_1\) равны и параллельны третьему отрезку \(АА_1\), следовательно: они равны и параллельны между собой, т. е. \(СС_1||BB_1\) и \(СС_1= BB_1\). Значит \(ВСС_1В_1\) — параллелограмм, и из этого получаем: \(ВС=В_1С_1\).
- Так как \(АВ=А_1В_1, AС =A_1С_1\) и \(СB=С_1B_1\), выясняем, что ΔABС и \(ΔA_1B_1С_1\) равны по трем сторонам, и поэтому \(А=А_1.\)
Угол между прямыми
Свойство пересекающихся прямых
Если две любые прямые лежат в одной плоскости и пересекаются, то они образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла. Углом между прямыми называют тот из углов, который не больше любого из трех остальных, очевидно, что он больше 0° и меньше либо равен 90°.
Угол между скрещивающимися прямыми
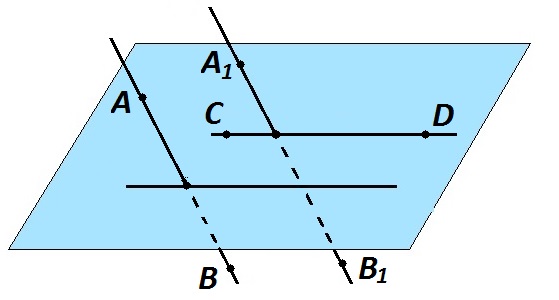
Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, параллельными заданным скрещивающимся прямым.
Угол между скрещивающимися прямыми АВ и СD равен \(∠А_1СD\) между \(А_1В_1\) и СD, если \(АВ||А_1В_1.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так