Основные законы логической алгебры

Что такое алгебра логики

С помощью этого понятия производятся вычисления, упрощения и преобразования с исходными суждениями.

Основные законы алгебры логики

Законы алгебры высказываний представляют собой тавтологии и также называются теоремами. Запись законов раздела математической логики осуществляется в виде эквивалентных формул. 

Закон тождества

Теорема представлена в виде формулы: A=A.

Рассматриваемый закон гласит, что любое высказывание тождественно самому себе. При рассуждении недопустима подмена одной мысли или понятия другими. В противном случае может возникнуть логическая ошибка.

Закон непротиворечия

Записывается в виде: \(A\&Ā=0\)

Рассматриваемая теорема означает, что суждение в конкретный момент времени может иметь или истинное, или ложное значение, третье исключено.

Закон исключенного третьего применяется только в определенных рассуждениях, где стоит формулировка «или –или».

В данном случае противоречие объясняется ссылкой суждения на самого себя. Возникающий в этом примере парадокс является доказательством того, что рассматриваемый закон не всегда применим. 

Закон двойного отрицания

Записывается в виде \(\overset=A=A\)

Означает, что при двойном отрицании исходного суждения в итоге получится оно же.

Свойства констант

Отрицание лжи есть истина:

\(A\cup0=A\)

\(A\cup1=1\)

Отрицание истины есть ложь:

\(A\&0=0\)

Закон идемпотентности

Теорема идемпотентности – это закон, дающий возможность исключить повторяющиеся суждения.

В записи данный закон выглядит так:

\(A\cup A=A\)

\(A\&A=A\)

Закон коммутативности

Рассматриваемая теорема применяется для выражений, связанных союзами «и», «или». Перемена мест высказываний в них не влияет на результат рассуждения.

\(A\cup B=B\cup A\)

\(А\&В=В\&А\)

Закон ассоциативности

Теорема утверждает, что логическое сложение и умножение ассоциативно, то есть при наличии в выражении лишь конъюнкции или лишь дизъюнкции можно опускать скобки:

\(A\cup(B\cup C)=(A\cup B)\cup C\)

\(А\&(В\&C)=(A\&В)\&С\)

Законы дистрибутивности

Рассматриваемая теорема является правилом раскрытия скобок при конъюнкции и дизъюнкции. 

Дистрибутивность логического сложения относительно логического умножения имеет значение – А или (В и С) есть тоже самое, что А или В и А или С – и записывается формулой:

\(A\cup(B\&C)=(A\cup B)\&(A\cup C)\)

Дистрибутивность логического умножения над логическим сложением читается как – А и (В или С) есть тоже самое, что А и В или А и С – и имеет вид:

\(А\&(B\cup C)=(A\;\&\;B)\cup(А\&C)\)

Закон поглощения

Теорема, при которой верны следующие равенства:

• для конъюнкции

\(A\cup(A\&B)=A\)

• для дизъюнкции

\(A\&(A\cup B)=A\)

Законы де Моргана

Законы общей инверсии названы в честь английского логика Августа де Моргана. Теорема для конъюнкции читается как – отрицание суждения «А и В» эквивалентно суждению «не-А или не-В» – и выглядит так:

\(\overline{A\&B}=\overline A\cup\overline B\)

Закон де Моргана для дизъюнкции означает, неверно, что А и В, если и только если неверно А и неверно В. Данное выражение можно записать в виде формулы:

\(\overline{A\cup B}=\overline A\&\overline B\)

Формы представления функций алгебры логики

Существует три способа представления выражений:

• в виде таблицы истинности;
• аналитическая форма;
• логическая форма.

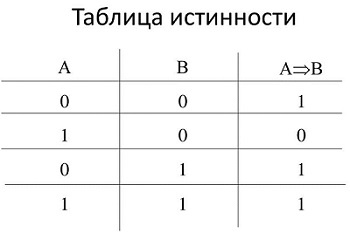
Таблица истинности 

При этом способе комбинации логических переменных они расположены в порядке возрастания их двоичного номера. Наборы переменных обозначаются числами от нуля до 2n − 1, где n – количество переменных функции. При наличии значений на всех комбинациях функция называется полностью определенной.

Аналитическое выражение

Рассмотрение данной формы невозможно без введения новых понятий.

• терм – компонент выражения;
• ранг терма – число переменных в терме;
• дизъюнктивный терм (макстерм) – логическое сложение произвольного количества попарно независимых переменных;
• конъюнктивный терм (минтерм) – логическое умножение произвольного количества попарно независимых переменных. 

В аналитической записи используют две формы выражения:

• дизъюнктивную нормальную форму (ДНФ)

\(f(a,b,c)=\overline ab\overline c+a\overline b+a\overline c+b\)

• конъюнктивную нормальную форму (КНФ)

\(f(X_1X_2X_3X_4)=(X_1+\overline{X_2}+X_3)(\overline{X_1}+\overline{X_2}+X_3+X_4)(X_1+X_2)\)

При условии, что все термы, составляющие нормальную форму, имеют одинаковый и максимальный ранг, который равен количеству переменных функции, форма называется совершенной. В такой форме минтерм – конституентная единицы, макстерм – конституентная нуля.

Совершенная дизъюнктивная форма (дизъюнкция конституент единицы) записывается так:

\(F(a,b,c)=\overline abc+abc+abc+ab\overline c\)

Совершенная конъюнктивная форма (конъюнкция конституент нуля) имеет вид:

\(F(a,b,c,d)=(a+b+\overline c+d)(\overline a+b+\overline c+d)(\overline a+\overline d+\overline c+d)\)

Аналитические формы полностью дуальны.

Числовая запись

Данный вид записи функций алгебры логики позволяет представить ее компактно.

Вид для совершенной дизъюнктивной нормальной формы:

\(f(a,b,c)=\vee(1,3,6,7)\)

Вид для совершенной конъюнктивной нормальной формы:

\(f(a,b,c)=\wedge(0,2,4,5)\)

Логические операции

Сложные логические суждения формируются из простых логических операций. Основные логические операции:

• конъюнкция или логическое умножение;
• дизъюнкция или логическое сложение;
• инверсия или логическое отрицание.

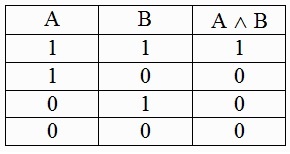
Конъюнкция

В основе логического умножения стоят два высказывания, в соответствие с которыми ставится новое суждение,  являющееся истиной лишь в том случае, когда оба исходных высказывания истинны.

Конъюнкция может быть записана следующими способами:

• A и B;
• A ⊥ B;
• A ⋅ B;
• A & B.

Дизъюнкция

При логическом сложении двух исходных суждений получается новое высказывание, ложное лишь в том случае, когда оба исходных суждения ложны.

Графическое обозначение дизъюнкции:

• A или B;
• A ⊦ B;
• A|B;
• A+B.

Инверсия

При логическом отрицании в соответствие каждому суждению ставится противоположное исходному высказывание.

Символическое представление:

• не А;
• ¬А;
• Ā.

Разложение в дизъюнкцию

Составление совершенных форм происходит по таблице истинности функции.

Правило для составления дизъюнкции конституент единицы: для каждой комбинации переменных, где функция истинна, записывается минтерм ранга n>, где переменные с нулевым значением в рассматриваемом наборе берутся с отрицанием. Все конъюнктивные термы объединяют дизъюнктивно. СДНФ для номеров N=1, 3, 6, 7:

\(f(a,b,c)=\overline a\overline bc+\overline abc+ab\overline c+abc\)

Разложение в конъюнкцию

Правило составления конъюнкции конституент нуля по таблице истинности: для каждого набора переменных, где функция имеет ложное значение, записывают дизъюнктивный терм ранга n, в котором переменные с единичными значениями на данной комбинации берутся с отрицанием. Все макстермы объединяют конъюнктивно. СКНФ для номеров наборов N=0, 2, 4, 5:

\(f(a,b,c)=(a+b+c)(a+\overline b+c)(\overline a+b+c)(\overline a+b+\overline c)\)

Как составить таблицу истинности

Алгоритм построения таблицы истинности:

1. Определить число переменных функции.
2. Посчитать, сколько всего операций в выражении.
3. Учесть скобки и установить порядок выполнения логических операций.
4. Узнать количество столбцов в таблице путем сложения количества переменных и числа операций.
5. В шапке таблицы записать переменные и операции в установленном в п.3 порядке.
6. Определить количество строк в таблице (без шапки) по формуле m=2n.
7. Выписать комбинации входных переменных, представленных в виде целого ряда двоичных чисел от 0 до 2n−1 с разрядом n.
8. Заполнить столбцы таблицы, последовательно совершая логические операции.