Первый и второй замечательные пределы

Первый замечательный предел

Понятие «замечательные пределы» используется в математике для объяснения известных тождеств со взятием предела.

Данная лемма служит основой для вычисления производных тригонометрических функций, которые содержат синус, арксинус, тангенс и арктангенс.

В записи тождество математического анализа имеет следующий вид:

\(\lim_{x\rightarrow0}\frac{\sin\left(x\right)}x=1\)

Доказательство

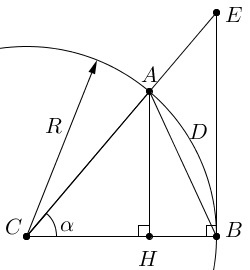
Предположим, что A и B принадлежат окружности с центром в точке С и радиусом, равным R. Отсюда следует, что |CA| = |CB| = R. Из точки А опустим перпендикуляр АН к отрезку СВ, следовательно, АН — это высота треугольника АВС. Далее проведем перпендикуляр ВЕ к стороне ВС до пересечения с прямой СА в точке Е. Обозначим угол между отрезками СА и СВ как α, выраженный в радианах:

\(\alpha=\frac{\left|\overset\frown{ADB}\right|}R\)

Здесь \(\;\left|\overset\frown{ADB}\right|\;-\;длина\;дуги\;окружности.\)

Доказательство при 0<α<π/2

Так как длина стороны АВ — это самое краткое расстояние между А и В, то модуль отрезка АВ меньше модуля дуги ADB или:

\(\left|AB\right|<\left|\overset\frown{ADB}\right|\)

Из прямоугольного треугольника АВН имеем:

\(\left|AH\right|=\sqrt{\left|AB\right|^2-\left|BH\right|^2}<\left|AB\right|<\left|\overset\frown{ADB}\right|\)

\(\left|AH\right|<\left|\overset\frown{ADB}\right|\)

Подставим:

\(\left|AH\right|=R\sin\left(\alpha\right),\;\left|\overset\frown{ADB}\right|=R\alpha\)

\(R\sin\left(\alpha\right)<R\alpha\)

Разделим на число с положительным значением Rα:

\((a)\;\frac{\sin\left(\alpha\right)}\alpha<1\)

Для дальнейшего доказательства необходима лемма.

Согласно этому утверждению:

\(\left|\overset\frown{ADB}\right|<\left|EB\right|\)

Подставим в это неравенство:

\(\left|\overset\frown{ADB}\right|=R\alpha\)

\(\left|EB\right|<R\;\tan\left(\alpha\right):\)

\(R\alpha<R\;\tan\left(\alpha\right)=R\frac{\sin\left(\alpha\right)}{\cos\left(\alpha\right)}\)

Выполним умножение на положительное число:

\(\frac{\cos\left(\alpha\right)}{R\alpha}:\)

\((б)\;\cos\left(\alpha\right)\;<\frac{\sin\left(\alpha\right)}\alpha\)

Из (а) и (б) следует, что при 0<α<π/2:

\((в)\;\cos\left(\alpha\right)\;<\frac{\sin\left(\alpha\right)}\alpha<1\)

Доказательство при отрицательных значениях: −π/2<α<0

В этом случае β=−α, β>0. Подставим в двойное неравенство (в) и воспользуемся четностью косинуса и нечетностью синуса:

\(\cos\left(\beta\right)\;<\frac{\sin\left(\beta\right)}\beta<1\)

\(\cos\left(-\alpha\right)\;<\frac{\sin\left(-\alpha\right)}{-\alpha}<1\)

\(\cos\left(\alpha\right)\;<\frac{-\sin\left(\alpha\right)}{-\alpha}<1\)

\(\cos\left(\alpha\right)\;<\frac{\sin\left(\alpha\right)}\alpha<1\)

Отсюда следует, что двойное неравенство (в) выполняется для положительных и отрицательных значений 0<|α|<π/2:

\((г)\;\cos\left(\alpha\right)\;<\frac{\sin\left(\alpha\right)}\alpha<1\)

при 0<|α|<π/2.

Из-за непрерывности функции косинус:

\(\lim_{\alpha\rightarrow0}\cos\left(\alpha\right)=\cos\left(0\right)=1\)

Перейдем в неравенстве (г) к пределу α→0. Используем теорему о промежуточной функции и получим:

\(\lim_{\alpha\rightarrow0}\frac{\sin\left(\alpha\right)}\alpha=1\)

Теперь обозначим α буквой x и получим:

\(\lim_{x\rightarrow0}\frac{\sin\left(x\right)}x=1\)

Первый замечательный предел доказан.

Примеры решений

Задача 1

Найти предел:

\(\lim_{x\rightarrow0}\frac{\tan\left(x\right)}{2x}\)

Решение

В исходное выражение подставим вместо переменной x значение, равное нулю. Выполнив это, получим:

\(\left[\frac00\right]\)

Далее выполним преобразования, чтобы применить первый замечательный предел. Для этого тангенс представим в виде отношения синуса к косинусу:

\(\lim_{x\rightarrow0}\frac{\tan\left(x\right)}{2x}=\lim_{x\rightarrow0}\frac{\frac{\sin\left(x\right)}{\cos\left(x\right)}}{2x}=\lim_{x\rightarrow0}\frac{\sin\left(x\right)}{\cos\left(x\right)}\times\frac1{2x}=\lim_{x\rightarrow0}\frac{\sin\left(x\right)}{2x}\times\frac1{\cos\left(x\right)}\)

Свойства пределов позволяют вынести константу за знак предела, а также произвести замену предела произведения произведением пределов (при существовании последних):

\(\lim_{x\rightarrow0}\frac{\tan\left(x\right)}{2x}=\lim_{x\rightarrow0}\frac{\sin\left(x\right)}{2x}\times\frac1{\cos\left(x\right)}=\frac12\lim_{x\rightarrow0}\frac{\sin\left(x\right)}x\times\lim_{x\rightarrow0}\frac1{\cos\left(x\right)}\)

Первый предел последнего выражения является первым замечательным пределом, который равен:

\(\lim_{x\rightarrow0}\frac{\sin\left(x\right)}x=1\)

Подставим во второй предел x=0:

\(\lim_{x\rightarrow0}\frac{\tan\left(x\right)}{2x}=\frac12\lim_{x\rightarrow0}\frac{\sin\left(x\right)}x\times\lim_{x\rightarrow0}\frac1{\cos\left(x\right)}=\frac12\times1\times\frac1{\cos\left(0\right)}=\frac12\times1\times\frac11=\frac12\)

Ответ: \(\lim_{x\rightarrow0}\frac{\tan\left(x\right)}{2x}=\frac12.\)

Второй замечательный предел

Рассматриваемую лемму можно записать в виде формулы:

\(\lim_{x\rightarrow\infty}\left(1+\frac1x\right)^x=e\)

В данном случае х — действительное число; e — число Эйлера.

Доказательство

Чтобы доказать указанное утверждение, будем применять факт, что последовательность

\(x_n=\left(1+\frac1n\right)^n\)

строго возрастает и ее конечный предел равен величине е:

\(\lim_{n\rightarrow\infty}x_n=e\)

Для начала рассмотрим правый предел:

\(\lim_{x\rightarrow+\infty}\left(1+\frac1x\right)^x\)

Чтобы он существовал, необходимо существование такой окрестности +∞, где функция является определенной и имеет вид:

\(f(x)=\left(1+\frac1x\right)^x\)

В конкретном случае f(x) определена при x>0. Можно выбрать любую окрестность. Для удобства примем x≥1.

Пусть n(x) — это функция, обозначающая целую часть числа x, к примеру: n(1)=1, n(1,2)=1, n(2,02)=2, n(3)=3. Указанная функция неубывающая. 

Рассмотрим сложную функцию:

\(g(x)=\left(1+\frac1{n(x)}\right)^{n(x)}\)

Приведем доказательство того, что при условии x→+∞ она имеет предел, равный числу Эйлера:

\(\lim_{x\rightarrow+\infty}g(x)=e\)

Так как последовательность 

\(x_n=\left(1+\frac1n\right)^n\)

строго возрастающая, а n(x) — неубывающая, сложная функция g(x) также не убывает.

В этом случае по теореме о пределе монотонной функции данная сложная функция обладает конечным, либо бесконечным пределом при условии x→+∞:

\(\lim_{x\rightarrow+\infty}g(x)=A\)

Покажем, что А=e с применением определения предела функции по Гейне. Согласно ему: если g(x) имеет предел при x→x₀: 

\(\lim_{x\rightarrow x_0}g(x)=A\)

В этой ситуации для любой последовательности \({y_n}\), сходящейся к x₀, последовательность \({g(y_n)}\) сходится к А:

\(\lim_{n\rightarrow\infty}g(x)=A\)

Возьмем последовательность y_n=n, которая сходится к +∞, тогда:

\(\lim_{n\rightarrow\infty}g(x)=A\)

Поскольку последовательность \({g(y_n)}\) совпадает с \({x_n}\):

\(g(y_n)=\left(1+\frac1{n(y_n)}\right)^{n(y_n)}=\left(1+\frac1{n(n)}\right)^{n(n)}=\left(1+\frac1n\right)^n=x_n\)

Поэтому предел данной последовательности равен:

\(\lim_{n\rightarrow\infty}g(y_n)=\lim_{n\rightarrow\infty}x_n=e\)

В результате приходим к равенству А=е:

\((a)\;\lim_{x\rightarrow+\infty}g(x)=\lim_{x\rightarrow+\infty}\left(1+\frac1{n(x)}\right)^{n(x)}=e\)

Подставим x=t+1. Отметим, что x(n)=n(t+1)=n(t)+1. Заменим переменную t на x и получим:

\((б)\;\lim_{x\rightarrow+\infty}\left(1+\frac1{n(x)+1}\right)^{n(x)+1}=e\)

Далее воспользуемся условием n(x)≤x≤n(x)+1, значит:

\(\left(1+\frac1{n(x)+1}\right)^{n(x)}\leq\left(1+\frac1{n(x)+1}\right)^x<\left(1+\frac1x\right)^x\leq\left(1+\frac1{n(x)}\right)^x<\left(1+\frac1{n(x)}\right)^{n(x)+1}\)

\((в)\;\left(1+\frac1{n(x)+1}\right)^{n(x)}<\left(1+\frac1x\right)^x<\left(1+\frac1{n(x)}\right)^{n(x)+1}\)

Заметим, что:

\(\lim_{x\rightarrow+\infty}\left(1+\frac1{n(x)}\right)=1\)

\(\lim_{x\rightarrow+\infty}\left(1+\frac1{n(x)+1}\right)=1\)

Используем арифметические свойства предела функции и пределы (а) и (б):

\(\lim_{x\rightarrow+\infty}\left(1+\frac1{n(x)+1}\right)^{n(x)}=\lim_{x\rightarrow+\infty}\frac{\left(1+\frac1{n(x)+1}\right)^{n(x)+1}}{1+\frac1{n(x)+1}}=\frac e1=e\)

\(\lim_{x\rightarrow+\infty}\left(1+\frac1{n(x)}\right)^{n(x)+1}=\lim_{x\rightarrow+\infty}\left[\left(1+\frac1{n(x)}\right)\times\left(1+\frac1{n(x)}\right)^{n(x)}\right]=1\times e=e\)

Применим к (в) теорему о промежуточной функции и получим:

\(\lim_{x\rightarrow+\infty}\left(1+\frac1x\right)^x=e\)

Далее рассмотрим левый предел:

\(\lim_{x\rightarrow-\infty}\left(1+\frac1x\right)^x\)

Пусть x≤−2. Произведем подстановку x=−y  и получим y≥2. При x→−∞, y→+∞.

\(\left(1+\frac1x\right)^x=\left(\frac{x+1}x\right)^x=\left(\frac{-y+1}{-y}\right)^{-y}=\left(\frac{y-1}y\right)^{-y}=\left(\frac y{y-1}\right)^y=\left(\frac{y-1+1}{y-1}\right)^y=\left(1+\frac1{y-1}\right)^y=\left(1+\frac1{y-1}\right)\times\left(1+\frac1{y-1}\right)^{y-1}\)

Применим арифметические свойства предела функции:

\(\lim_{x\rightarrow-\infty}\left(1+\frac1x\right)^x=\lim_{y\rightarrow+\infty}\left[\left(1+\frac1{y-1}\right)\times\left(1+\frac1{y-1}\right)^{y-1}\right]=\lim_{y\rightarrow+\infty}\left(1+\frac1{y-1}\right)\times\lim_{y\rightarrow+\infty}\left(1+\frac1{y-1}\right)^{y-1}=1\times e=e\)

Так как и справа, и слева существуют равные пределы, то имеет место двусторонний предел:

\(\lim_{x\rightarrow\infty}\left(1+\frac1x\right)^x=e\)

Второй замечательный предел доказан.

Примеры решений

Задача 1

Вычислить предел:

\(\lim_{x\rightarrow1}\left(7-6x\right)^\frac x{3x-3}\)

Решение

Выражение 7−6x стремится к 1 при условии, что x→1, то есть:

\(\lim_{x\rightarrow1}\left(7-6x\right)=7-6\times1=1\)

Для показателя степени x/3x-3 получаем:

\(\lim_{x\rightarrow1}\frac x{3x-3}=\infty\)

Таким образом, в данном случае имеет место неопределенность вида 1 в степени бесконечности. Ее возможно раскрыть с применением второго замечательного предела.

Сначала отметим, что в формуле:

\(\lim_{x\rightarrow\infty}\left(1+\frac1x\right)^x=e\)

x стремится к бесконечности, а в формуле:

\(\lim_{t\rightarrow0}\left(1+t\right)^\frac1t=e\)

t стремится к нулю.

В данном примере x стремится к единице, поэтому для удобства введем еще одну переменную, стремящуюся либо к бесконечности, либо к нулю, чтобы воспользоваться одной из приведенных выше формул.

Пусть новая переменная y равна разности x−1. Поскольку x стремится к 1, то x−1 стремится к нулю, то есть y→0.

Подставим x=y+1 при y→0:

\(\lim_{x\rightarrow1}\left(7-6x\right)^\frac x{3x-3}=\begin{vmatrix}y=x-1;&\;x=y+1\\y\rightarrow0&\end{vmatrix}=\lim_{y\rightarrow0}\left(7-6\times\left(y+1\right)\right)^{{}^\frac{y+1}{3\left(y+1\right)-3}}=\lim_{y\rightarrow0}\left(1-6y\right)^{{}^\frac{y+1}{3y}}=\lim_{y\rightarrow0}\left(1+\left(-6y\right)\right)^{{}^\frac{y+1}{3y}}\\\)

Воспользуемся формулой:

\(\lim_{t\rightarrow0}\left(1+t\right)^\frac1t=e\)

Основание 1+t соответствует выражению в основании примера 1+(−6y). Исходя из формулы, показатель степени должен иметь вид 1/t, следовательно, необходимо привести показатель степени в примере к соотношению 1/−6y. Для этого умножим его на данную дробь. Компенсируем это действие с помощью дополнительного умножения на обратную дробь, то есть фактически на −6y:

\(\lim_{y\rightarrow0}\left(1-6y\right)^{{}^\frac{y+1}{3y}}=\lim_{y\rightarrow0}\left(1+\left(-6y\right)\right)^{{}^\frac{y+1}{3y}}=\lim_{y\rightarrow0}\left(1+\left(-6y\right)\right)^{{}^{\frac1{-6y}\times\left(-6y\right)\times\frac{y+1}{3y}}}=\lim_{y\rightarrow0}\left(\left(1+\left(-6y\right)\right)^\frac1{-6y}\right)^{-2\left(y+1\right)}\\\)

Поскольку:

\(\lim_{y\rightarrow0}\left(1+\left(-6y\right)\right)^{{}^\frac1{-6y}}=e\\\)

и

\(\lim_{y\rightarrow0}\left(-2\left(y+1\right)\right)=-2\\\)

значит:

\(\lim_{y\rightarrow0}\left(\left(1+\left(-6y\right)\right)^\frac1{-6y}\right)^{-2\left(y+1\right)}=e^{-2}=\frac1{e^2}\\\)

Ответ: \(\lim_{x\rightarrow1}\left(7-6x\right)^\frac x{3x-3}=\frac1{e^2}.\\\)

Следствия второго замечательного предела

Следствие 1

Для того, чтобы доказать первое следствие, произведем замену:

\(x=\frac1t,\;t=\frac1x\)

При подстановке получится следующее:

\(\left(1+x\right)^\frac1x=\left(1+\frac1t\right)^t\)

При условии, что x→0, t→∞:

\(\lim_{x\rightarrow0}\left(1+x\right)^\frac1x=\lim_{t\rightarrow\infty}\left(1+\frac1t\right)^t=e\)

Обратим внимание на то, что по факту F(x) представлена как сложная функция:

\(F(x)=\left(1+x\right)^\frac1x=f(t(x))\)

где:

\(f(t)=\left(1+\frac1t\right)^t\)

\(t(x)=\frac1x\)

Затем была применена теорема о пределе сложной функции.

Следствие 1 доказано.

Следствие 2

Убедимся, что \(\lim_{x\rightarrow0}\frac{a^x-1}x=\ln\left(a\right),\;a>0,\;a\neq0\)

Приведенная функция является обратной логарифмической. Исходя из этого, выполним преобразования:

\(\frac x{a^x-1}=\frac{\log_a\left(a^x\right)}{a^x-1}=\frac1{a^x-1}\log_a\left(1+a^x-1\right)=\log_a\left(1+a^x-1\right)^\frac1{a^x-1}\)

Теперь заменим переменную t=a^x−1. Вследствие непрерывности показательной функции:

\(\lim_{x\rightarrow0}\left(a^x-1\right)=a^0-1=1-1=0\)

Так как x≠0, a^x−1≠0, то:

\(\lim_{x\rightarrow0}\frac x{a^x-1}=\lim_{x\rightarrow0}\log_a\left(1+a^x-1\right)^\frac1{a^x-1}=\lim_{t\rightarrow0}\log_a\left(1+t\right)^\frac1t=\log_a\left(\lim_{t\rightarrow0}\left(1+t\right)^\frac1t\right)=\log_a\left(e\right)\)

В предпоследнем равенстве была использована непрерывность логарифмической функции и теорема о пределе непрерывной функции от функции. В последнем равенстве воспользовались следствием второго замечательного предела.

Отметим, что при подстановке функция F(x) была представлена как сложная:

\(F(x)=\log_a\left(1+a^x-1\right)^\frac1{a^x-1}=f(t(x))\)

где:

\(f(t)=\log_a\left(1+t\right)^\frac1t\)

\(t(x)=a^x-1\)

и применили теорему о пределе сложной функции.

Воспользовавшись арифметическими свойствами предела функции, имеем:

\(\lim_{x\rightarrow0}\frac{a^x-1}x=\lim_{x\rightarrow0}\frac1{\frac x{a^x-1}}=\frac1{\lim_{x\rightarrow0}\frac x{a^x-1}}=\frac1{\log_a\left(e\right)}=\ln\left(a\right)\)

Здесь применили свойство логарифма:

\(\log_a\left(b\right)=\frac1{\log_b\left(a\right)}\)

Считая, что a=e, имеем:

\(\lim_{x\rightarrow0}\frac{e^x-1}x=1\)

Что и требовалось доказать.

Следствие 3

Докажем следующее:

\(\lim_{x\rightarrow0}\frac{\log_a\left(1+x\right)}x=\frac1{\ln\left(a\right)},\;a>0,\;a\neq0\)

Преобразим выражение:

\frac{\log_a\left(1+x\right)}x=\frac1x\log_a\left(1+x\right)=\log_a\left(1+x\right)^\frac1x.

Функция определена при x>−1, x≠0. Логарифм непрерывен в данной области определения. Воспользуемся доказанным следствием 1 и теоремой о пределе непрерывной функции от функции:

\(\lim_{x\rightarrow0}\frac{\log_a\left(1+x\right)}x=\lim_{x\rightarrow0}\log_a\left(1+x\right)^\frac1x=\log_a\left(\lim_{x\rightarrow0}\left(1+x\right)^\frac1x\right)=\log_a\left(e\right)=\frac1{\ln\left(a\right)}\)

Также применено свойство логарифма:

\(\log_a\left(b\right)=\frac1{\log_b\left(a\right)}\)

Произведем подстановку a=e и получим:

\(\lim_{x\rightarrow0}\frac{\ln\left(1+x\right)}x=1\)

Следствие 3 доказано.

Следствие 4

Докажем справедливость равенства:

\(\lim_{x\rightarrow0}\frac{sh(x)}x=1\)

Воспользуемся определением гиперболического синуса и следствием 2. Преобразуем:

\(\lim_{x\rightarrow0}\frac{sh(x)}x=\lim_{x\rightarrow0}\frac{e^x-e^{-x}}{2x}=\frac12\lim_{x\rightarrow0}\frac{e^x-1-\left(e^{-x}-1\right)}x=\frac12\left(\lim_{x\rightarrow0}\frac{e^x-1}x+\lim_{x\rightarrow0}\frac{e^{-x}-1}{-x}\right)=\frac12\left(1+1\right)=1\)

Докажем:

\(\lim_{x\rightarrow0}\frac{th(x)}x=1\)

Применим определение гиперболического синуса и предыдущий предел:

\(\lim_{x\rightarrow0}сh(x)=\lim_{x\rightarrow0}\frac{e^x+e^{-x}}2=\frac{e^0+e^0}2=1\)

\(\lim_{x\rightarrow0}\frac{th(x)}x=\lim_{x\rightarrow0}\frac{sh(x)}{x\;ch(x)}=\lim_{x\rightarrow0}\left(\frac1{ch(x)}\times\frac{sh(x)}1\right)=1\times1=1\)

Докажем следующее:

\(\lim_{x\rightarrow0}\frac{arsh(x)}x=1\)

Заменим переменную t=arsh x. Тогда при х и t, стремящихся к нулю и не равных ему: x=sh arsh x=sh t.

\(\lim_{x\rightarrow0}\frac{arsh(x)}x=\lim_{t\rightarrow0}\frac t{sh(t)}=\lim_{t\rightarrow0}\frac1{\frac{sh(t)}t}=\frac11=1\)

Докажем, что верно равенство:

\(\lim_{x\rightarrow0}\frac{arth(x)}x=1\)

Заменим переменную t=arth x. Тогда при x и t, стремящихся к нулю и не равных ему, а также при |x|<1, x=th arth x=th t:

\(\lim_{x\rightarrow0}\frac{arth(x)}x=\lim_{t\rightarrow0}\frac t{th(t)}=\lim_{t\rightarrow0}\frac1{\frac{th(t)}t}=\frac11=1\)

Следствие 4 доказано.